Projective geometry (사영 기하학)
3D Rigid Body Motion은 모두 유클리드 기하학을 따릅니다.
사영대수학은 기초적인 유클리드 기하학과는 달리 사영공간과 몇 가지 기본적인 기하학적인 개념들로 구성되어 있습니다.
실제 3D 공간에 물리적인 객체 정보를 2D 이미지로 투영하는 것이 projection입니다.
즉, projective geometry는 N + 1 차원을 N 차원으로 차원 축소를 할 때 통용되는 기하학입니다.
Hierachies of geometries
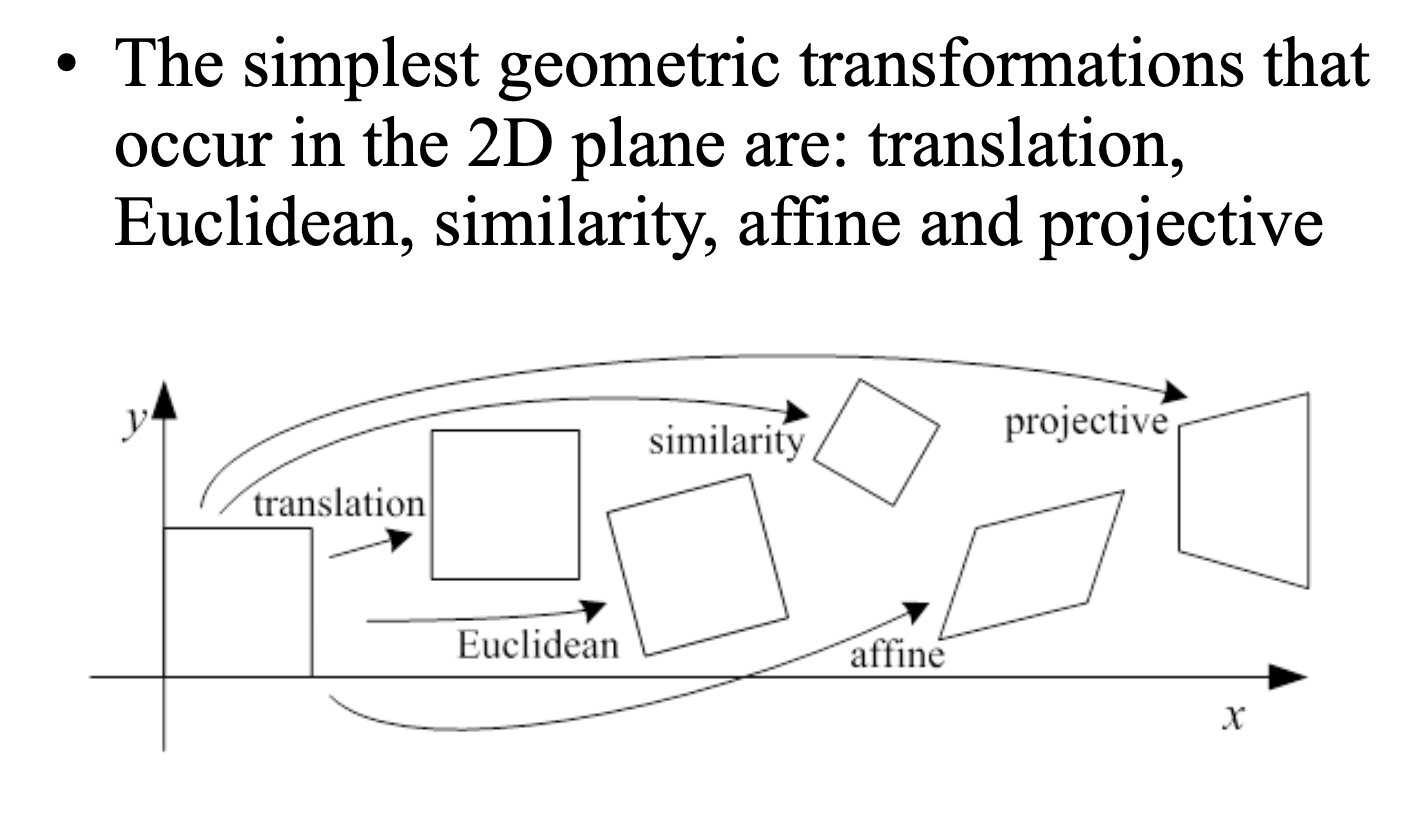

• Euclidean
> Rotation + Translation 표현 가능
• Similarity
> Euclidean transformation에서 uniform scaling 표현 가능
> Euclidean transformation에서 length 정보 손실
• Affine
> Similarity transformation에서 Non-uniform scaling + shear 표현 가능
> Similarity transformation에서 Angle / Length-ratio 정보 소실
• Projective
> Affine transformation에서 projection 표현 가능
> Affine transformation에서 incidence, cross-ratio 정보 손실
Homogeneous coordinates
: x라는 객체에 Homogeneous coordinates에 0이 아닌 어떤 스칼라값을 곱해도 coordinates는 같은 객체를 의미한다라고 합니다.
즉 x든, lambda * x든 x를 의미합니다.
Euclidean space에서 coordinate를 표현할 때 x, y 두 개만으로 표현했을 때는 cartesian coordinates라 하고,
projective space 에서 coordinate를 표현할 때 x, y, 1 세 개로 표현하는 것을 homogeneous coordiates라 합니다.

수많은 projective space scales 속에서 scale값이 1인 경우의 공간을 Euclidean space라고 합니다.
즉, 2D Euclidean space는 2D projective space 하위 개념이라고 볼 수 있습니다.
그럼 2D Euclidean space 속 좌표를 2D projective space에서 어떻게 표현할까요?
Euclidean space에 projection을 하면 0차원 정보가 됩니다. 즉, 점(포인트)이 된 것입니다.
Euclidean space는 N차원의 공간이며 N은 0이고,
projective space는 항상 N + 1차원을 가지니까 1차원을 갖는다고 말할 수 있습니다.
즉 직선으로 표현할 수 있습니다.
O_3 (0,0,0)에서 lambda * e를 곱한 값은 Euclidean 좌표에 존재하는 객체를 가리키는데 이때 lambda에 어떤 숫자가 들어와도 같은 객체를 나타냅니다. 이게 원근법이죠!

Matrix는 어떻게 homogeneous coordinate로 변환할까요?

Matrix도 scale 정보를 추가하면 됩니다.
SO(3)Matrix 같은 경우 가장 4*4 matrix의 오른쪽 아래에 1이라는 scale 정보가 있습니다.
1이라고 적혀있는 건 SO(3)matrix가 아직 Euclidean space에 있다는 것을 표현해주는 값입니다.
SE(3) Matrix는 SO(3) Matrix와는 다르게 4*4가 아닌 3*4입니다.
또한 SE(3) Matrix는 Homogeous coordinate로 표현하는 것이 관행인데 위 사진에 나와있는 건
Homogeous coordinate로 표현은 되었지만 아직도 Euclidean coorndate 작업이기 때문에 0 값이 채워진 걸 알 수 있습니다. Homogeous coordinate 값이었다면 다른 값이 채워졌겠죠.
추가 학습 자료
https://www.youtube.com/watch?v=PvEl63t-opM
http://www.yes24.com/Product/Goods/64454325
Photogrammetric Computer Vision: Statistics, Geometry, Orientation and Reconstruction - YES24
This textbook offers a statistical view on the geometry of multiple view analysis, required for camera calibration and orientation and for geomet...
www.yes24.com
'자율주행 데브코스 4기 TIL > SLAM' 카테고리의 다른 글
| 카메라 센서의 구조 (0) | 2023.02.24 |
|---|---|
| Camera projection (0) | 2023.02.23 |
| 3D Rigid Body Motion (0) | 2023.02.23 |
| SLAM 이론 공부 (0) | 2023.02.22 |
| SLAM (1) | 2023.02.21 |
 >
>
