Camera obscura(바늘구멍 사진기)는 인류가 projective geometry에 대해 수식적으로 연구를 할 수 있게 해준 계기가 되었습니다.
Camera obscura가 있었기 때문에 정확한 2D 이미지를 구할 수 있었고 2D 이미지를 측량해서 3D 세상과 비교함으로써 3D to 2D 매핑관계에 대한 수식을 발전 시킬 수 있었습니다.

x = P X
x: 3D world coordinate points
P: Projection matrix
X: 2D image coordinate points
Projection steps

1. World coordinate (3D) to Camera coordinate (3D) transformation

Rotation - 3*3 Matrix -> SO(3)
Translation - 3*1 Vector
Transformation - 4*4 Matrix -> SE(3)


2. Camera coordinate (3D) to Image coordinate (2D) Transformation
다음 사진은 world frame을 제거하고
Camera coordinate (3D) to Image coordinate (2D) Transformation을 보여줍니다.

Camera projection의 목표는 이 X_im을 수식적으로 표현하는 방법을 정확하게 찾는 것 입니다.
다음은 Camera frame 모습을 2D 단면적인 모습으로 보겠습니다.
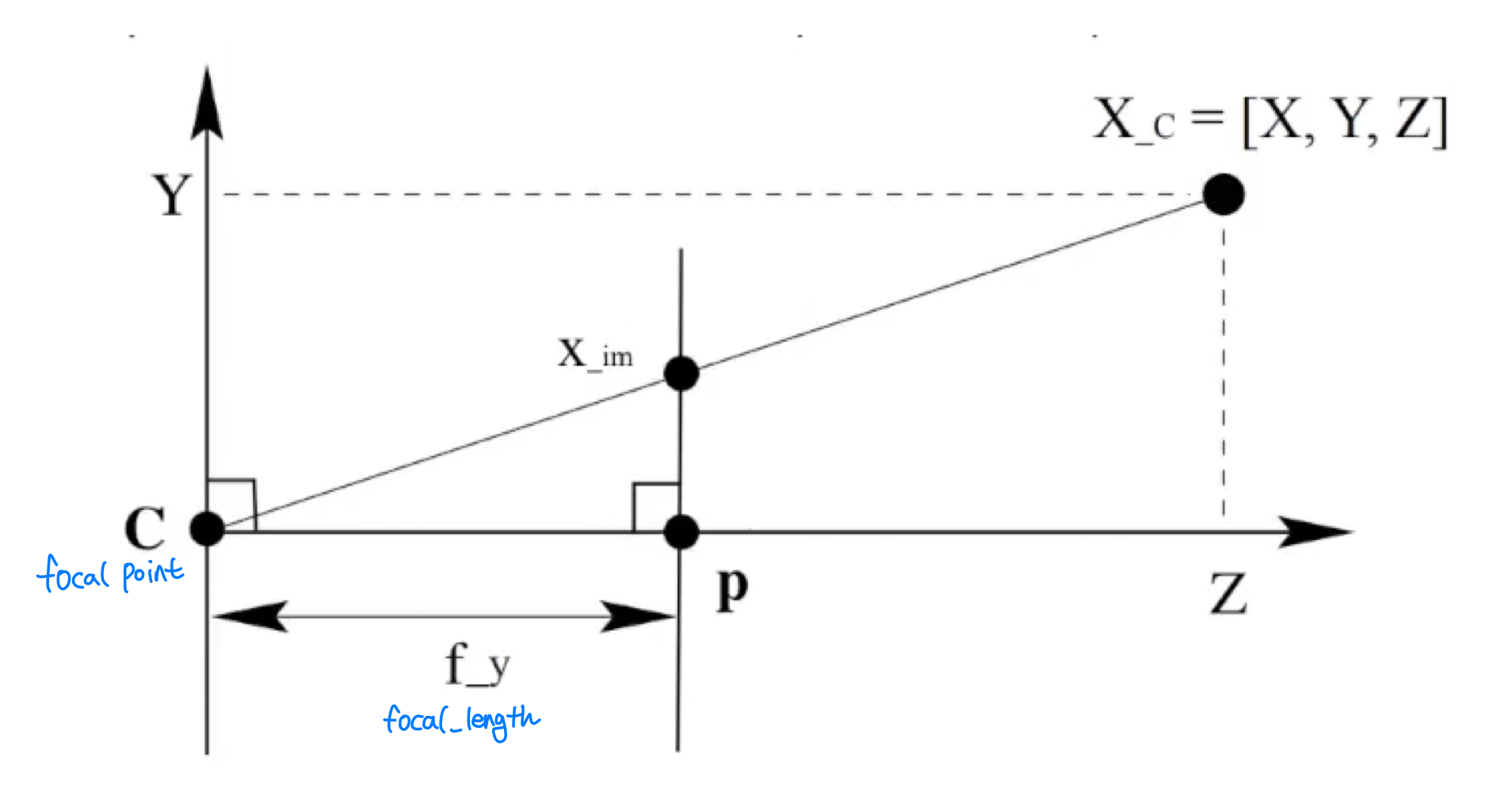
닮은비를 이용하여 주어진 정보로 X_im값을 구할 수 있습니다.
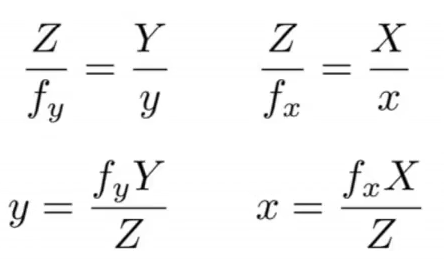
C를 기준으로 이미지의 중앙이 0,0인데 픽셀 정보로 나타내기 위해선 좌측 상단이 0,0이어야 합니다.
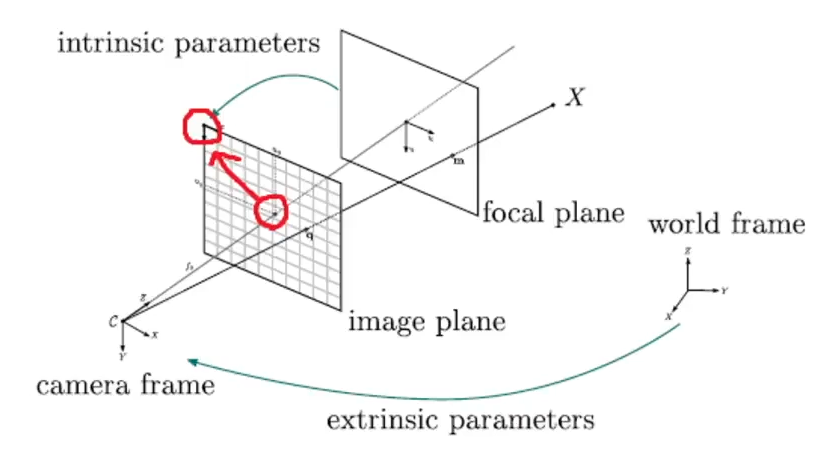
좌측 위부터 중앙까지의 거리를 알면 옮겨줄 수 있는데 카메라마다 공정 과정에서 중앙점이 안맞을 수 있기 때문에 camera calibration을 하는 이유가 이 때문입니다. 캘리브레이션을 진행하면 그 에러값(중앙에서 벗어난 오차값)을 알 수 있습니다.
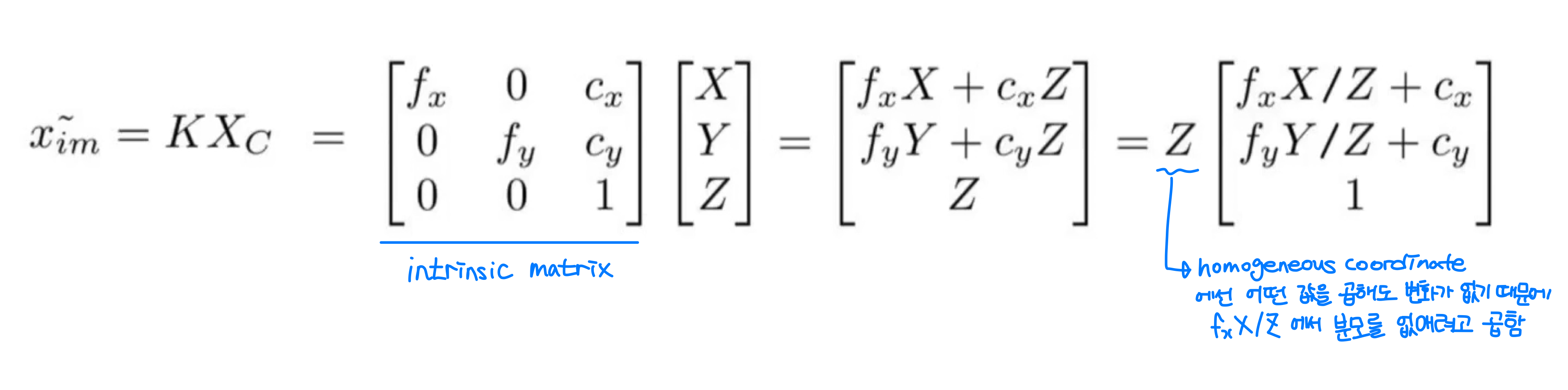
저기서 Intrinsic matrix가 하는 역할은 카메라 시점에서 본 3D 포인트 {X, Y, Z}를 2D 이미지상의 픽셀 위치로 맺히게 합니다.
본 내용은 자율주행 데브코스 장형기 강사님의 강의 내용을 요약한 글임을 밝힙니다.
'자율주행 데브코스 4기 TIL > SLAM' 카테고리의 다른 글
| Epipolar Geometry (0) | 2023.02.27 |
|---|---|
| 카메라 센서의 구조 (0) | 2023.02.24 |
| Projective geometry (0) | 2023.02.23 |
| 3D Rigid Body Motion (0) | 2023.02.23 |
| SLAM 이론 공부 (0) | 2023.02.22 |
 >
>
