
Rigid Body
(강체 ; 물리학에서 형태가 고정되어 변하지 않는 물체)
> Position = { tx, ty, tz }
> Orientation = { Rx, Ry, Rz }
> Pose = Orientation + Position
> 6 Degrees of Freedom = 3D Orientation + 3D Position = { tx, ty, tz, Rx, Ry, Rz }
Coordinate transformation ( Camera -> World )
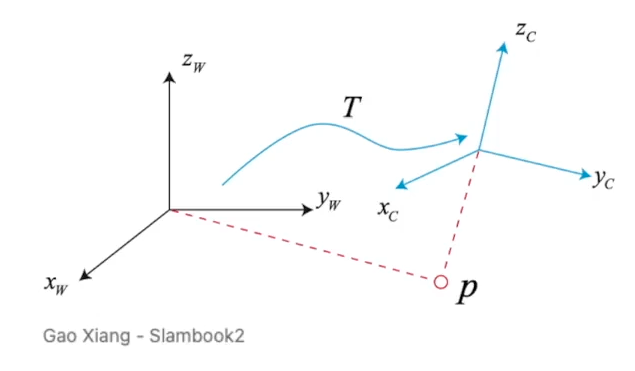
카메라 좌표계 { tx, ty, tz, Rx, Ry, Rz}를 어떻게 월드 좌표계 {?, ?, ?, ?, ?, ?, ?}로 바꿀 수 있을까?
Orientation{Rx, Ry, Rz}: Rotation(회전값) 이용
Position{tx, ty, tz} : Translation(이동값) 이용
Coordinate transform을 하기 위해서는 2개의 coordinate system 간의 이동이 필요합니다.
이걸 Rigid body motion 이라고 합니다.
3D -> 3D transformation (Rigid body motion)
: Euclidean transformation
- Euclidean world -> Euclidean world
- Cartesian coodinate -> Cartesian coodinate
coordinate source : https://www.cours-et-exercices.com/2016/01/modelisation-cinematique-des-liaisons.html
Rotation(회전) 표현법
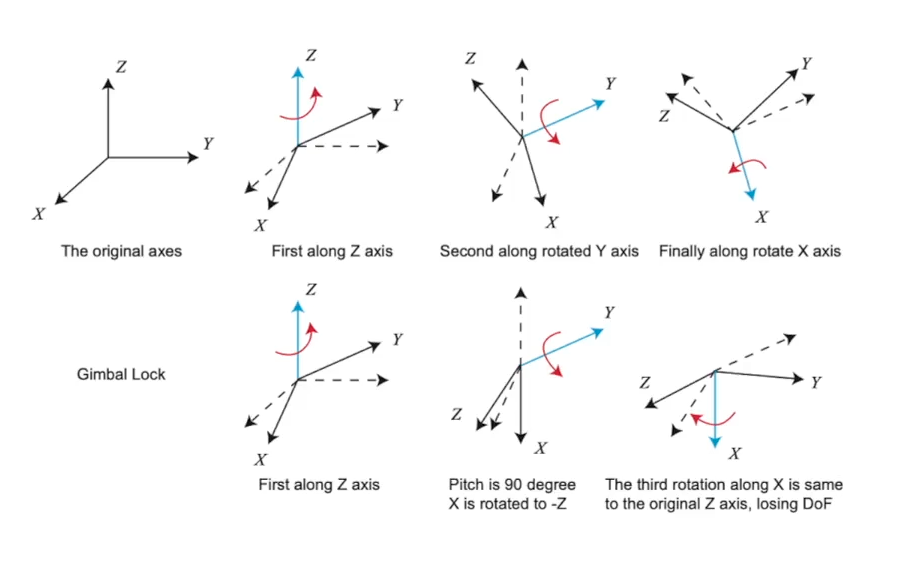
•Euler Angle
-장점: 이해하기 쉬움.
-단점: 최적화가 어려움, gimblock (Singularity problem)
•Axis-angle
(= Angle-axis, Rotation vector, Rodrigues angle, ...)
- Rotation axis -> e
- Rotation angle -> theta
- Rotation vector = e * theta
- Axis-angle <-> Rotation matrix
• Rodrigues formula(Axis-angle로부터 Rotation matrix 변환식)
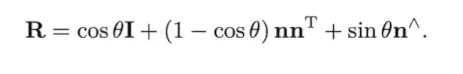

•Quaternion
3차원 좌표로 나타내면 Singularity problem이 발생
문제가 발생하지 않은 최소 차원인 4차원으로 표현하자는 아이디어.

4개의 파라미터로 3D 세상을 singularity 없이 표현할 수 있게 되었습니다.
즉 gimblock 문제가 없고, 미분이 가능합니다.
하지만 쿼터니안 값만 보고는 어디를 위치하는지 이해하기 어렵다는 단점이 있습니다.
•SO(3) Rotation matrix
(Special Orthogonal Matrix (3D) - SO(3)
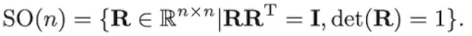
-회전만 시켜주는 matrix
-회전만 시켜주는 matrix는 회전 후에도 기존 x, y, z축이 수직(Orthogonality)을 유지한다는 특성이 있습니다.
-이 matrix의 Determinant 1이 되어야 합니다.
- SO(3) * SO(3) transpose = Identity Matrix
-최적화하기 위해 SO(3)matrix를 바로 사용하기에는 어렵다고 합니다. 미분하면 jacobian matrix가 나오는데 이걸 가지고 iteration 을 했었을 때 그 결과가 SO(3)와 동일한 성질을 가질지는 몰라 어렵기도 합니다.
- 미분 가능 형태는 Log map / Exponential map을 통한 Lie algebra 방법이 있습니다.

Translation(이동) 표현법
회전표현법과 다르게 단순히 벡터로 표현하면 됩니다. (단, 단위(mm, m, cm, ...) 를 맞춰야 합니다.)
• SE(3) Transformation matrix
(Special Euclidean Group (3D))
: 이동과 회전을 동시에 표현하는 방법
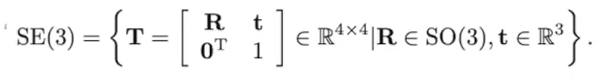
-4*4 행렬을 가짐

'자율주행 데브코스 4기 TIL > SLAM' 카테고리의 다른 글
| 카메라 센서의 구조 (0) | 2023.02.24 |
|---|---|
| Camera projection (0) | 2023.02.23 |
| Projective geometry (0) | 2023.02.23 |
| SLAM 이론 공부 (0) | 2023.02.22 |
| SLAM (1) | 2023.02.21 |
 >
>
