다익스트라 알고리즘이란?
: 그래프에서 엣지(노드) 간에 최단 거리(가중치 합 최소)를 구하는 알고리즘
그래프 알고리즘 문제에도 많이 쓰이는 알고리즘 중에 하나이며,
실생활에선 네비게이션 알고리즘에도 쓰여 알아두면 좋은 알고리즘이다.
알고리즘 이해
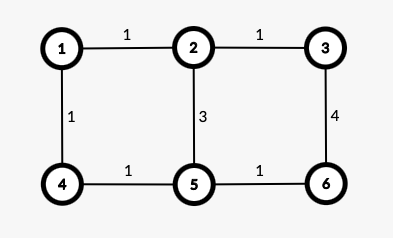
노드 간의 거리를 비교해 나가면서 최단 경로를 구해야하기 때문에 거리를 저장 시켜둘 필요가 있다.
노드 개수가 6개이므로 ,
크기가 6인 1차원 배열을 2개 만들어 (거리 정보와 방문 여부)를 저장시켜준다.
int distance[7];
bool visited[7] = {0,};배열은 인덱스 0번부터 시작하지만 쓴이는 인덱스 0번을 비우고 인덱스와 노드값을 동일하게 사용하려고 7개의 원소를 받는다고 하였다.
우리는 최종 거리에 대한 최솟값을 구해야하기 때문에 각각의 원소들을 0이 아닌 무한(Infinite)으로 초기화 해준다.
무한을 나타내기 위해선 자료형 크기 범위 내에 엄청 큰 숫자를 입력 해주기만 하면 된다.
#define INF 1000000001| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 거리 | X | 0 | INF | INF | INF | INF | INF |
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 방문여부 | X | false | false | false | false | false | false |
알고리즘 순서
1. 출발 지점으로 두고싶은 노드를 정한다. (노드 1)
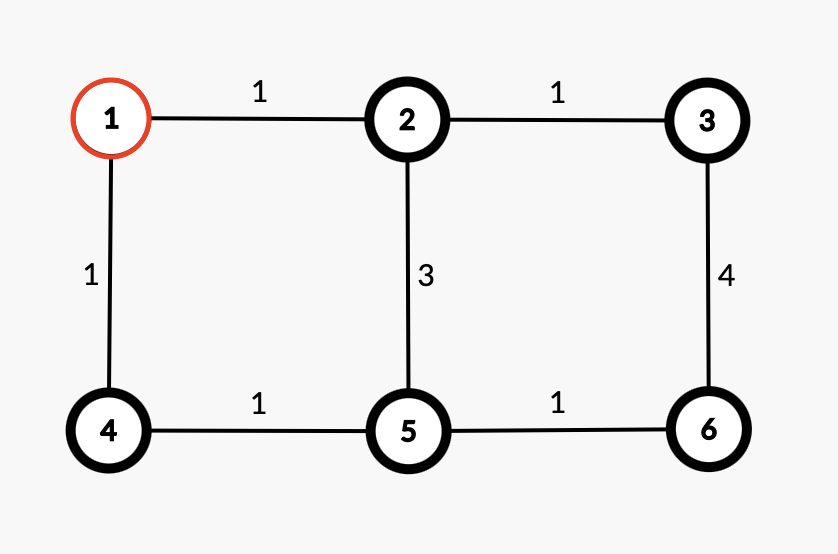
노드 1과 바로 연결돼있는 노드는 다음 표와 같다.
| 노드 | 거리 |
| 2 | 1 |
| 4 | 1 |
2. 거리 정보를 distance 배열에 저장시켜준다.
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 거리 | X | 0 | 1 | INF | 1 | INF | INF |
기존 저장돼있는 값과 새로 갱실할 거리의 값을 비교하여 더 작은 값을 distance배열에 저장시켜준다.
INF와 1을 비교하였을 때 당연히 1이 더 작으므로 1로 갱신한다.
3. 다음 노드를 방문하여 해당 노드를 거쳐 가는 경로의 거리를 비교해준다.
방문이 완료된 노드1은 방문했다는 표시한다.
다음 노드를 선택하는 방법은 방문하지 않은 노드들 중에 거리에 대한 최솟값을 가지는 노드를 선택.
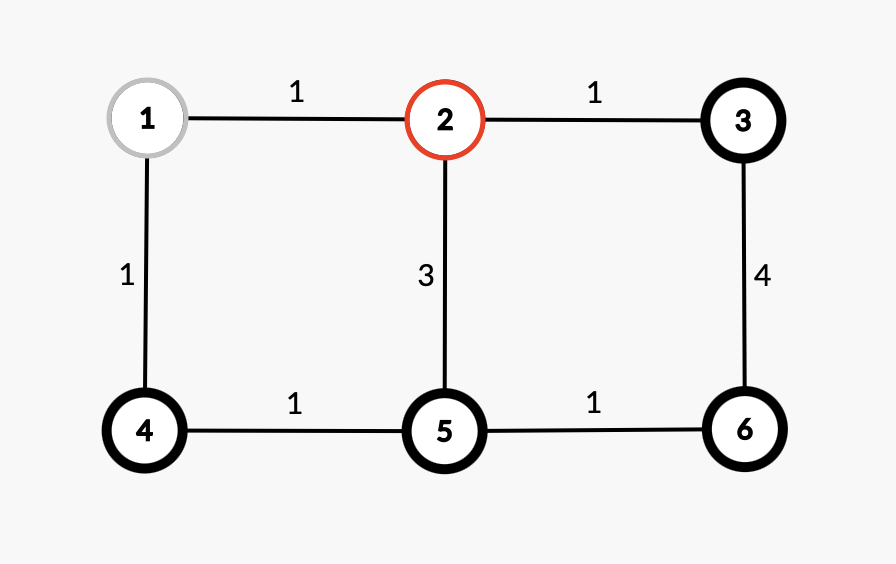
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 방문여부 | X | true | false | false | false | false | false |
노드 2와 연결된 노드는 다음과 같다.
| 노드 | 거리 | 노드를 거쳐간 거리 |
| 3 | 1 | 1+1 |
| 5 | 3 | 1+3 |
노드 2를 거쳐 다른 노드로 가는 비용은 각각 이렇다.
(노드 1-노드2 거리) + (노드 2-노드3 거리) = 2
(노드 1-노드2 거리) + (노드 2-노드5 거리) = 4
노드3과 노드5의 거리는 각각 2,4이며 distance 배열에 저장돼있는 INF값 보다 작으므로 갱신한다.
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 거리 | X | 0 | 1 | 2 | 1 | 4 | INF |
노드2에 대한 작업이 끝났으므로 방문 표시를 해주고 다음 노드(4)를 선택한다.
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 방문여부 | X | true | true | false | false | false | false |
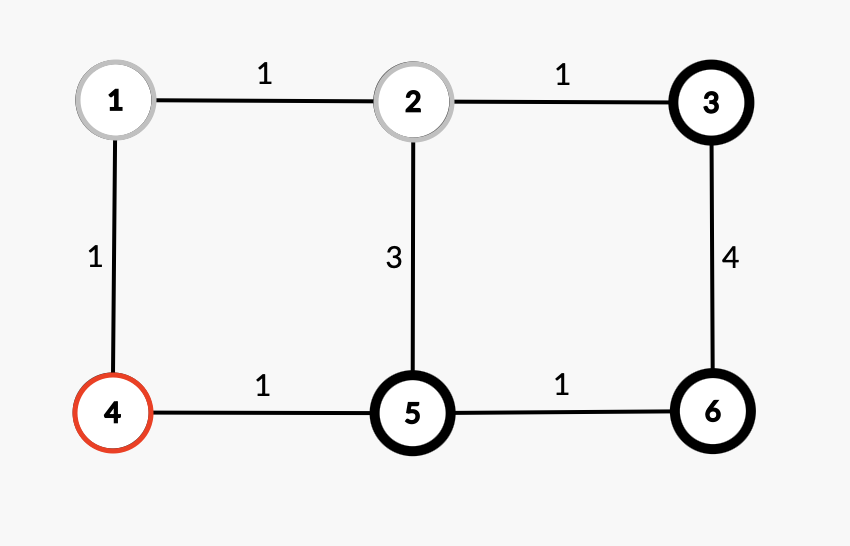
| 노드 | 거리 | 노드를 거쳐간 거리 |
| 5 | 1 | 1+1 |
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 거리 | X | 0 | 1 | 2 | 1 | 4 | INF |
기존 저장 돼있는 값 4보다 2가 더 작으므로 2로 갱신해준다.
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 거리 | X | 0 | 1 | 2 | 1 | 2 | INF |
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 방문여부 | X | true | true | false | true | false | false |
노드 3 선택
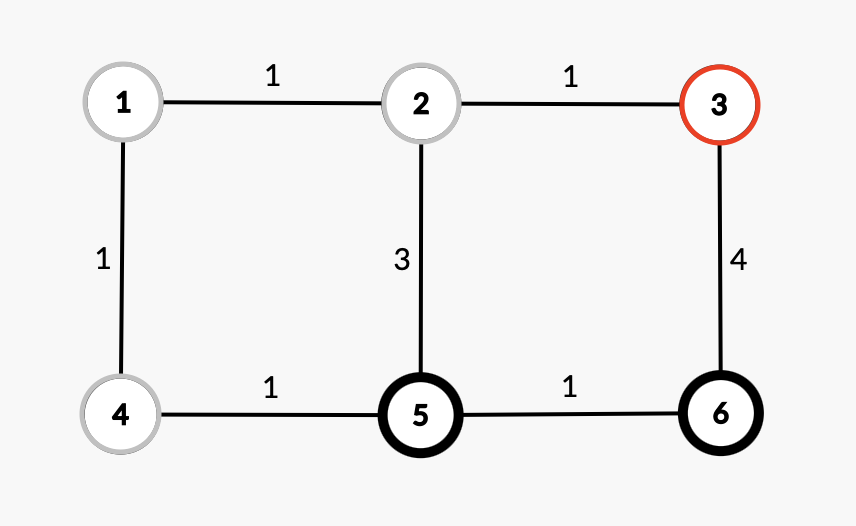
| 노드 | 거리 | 노드를 거쳐간 거리 |
| 6 | 1 | 2+4 |
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 거리 | X | 0 | 1 | 2 | 1 | 4 | INF |
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 거리 | X | 0 | 1 | 2 | 1 | 2 | 6 |
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 방문여부 | X | true | true | true | true | false | false |
노드5로 이동
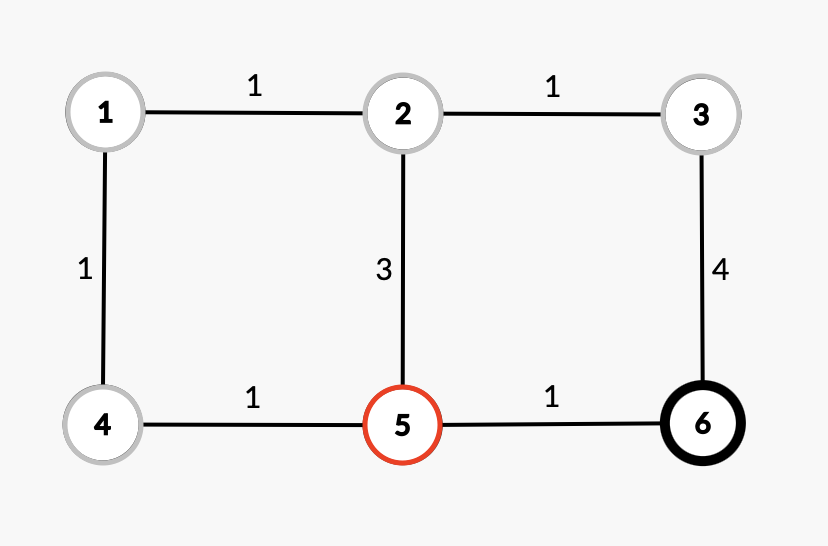
| 노드 | 거리 | 노드를 거쳐간 거리 |
| 6 | 1 | 2+1 |
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 거리 | X | 0 | 1 | 2 | 1 | 4 | 6 |
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 거리 | X | 0 | 1 | 2 | 1 | 2 | 3 |
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 방문여부 | X | true | true | true | true | true | false |
노드 6은 인접 노드가 없으므로 작업을 끝마치면 된다.
최종적으로 각 노드 위치에 대한 최단 경로 값들이 나오게 된다.
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 거리 | X | 0 | 1 | 2 | 1 | 2 | 3 |
#include<iostream>
#include<queue>
#include<vector>
#define INF 100000001 //무한을 나타내는 수
using namespace std;
vector<pair<int, int> > v[7]; //노드 정보를 저장하는 벡터
int d[7] = {0,}; //노드 거리를 저장하는 배열
void dijkstra(int n) {
d[n] = 0; //자기 자신에 대한 거리이므로 0으로 초기화
priority_queue<pair<int, int> >pq; //거리가 가까운 노드부터 처리하기 위해 우선순위 큐 사용
pq.push(make_pair(n,0)); //시작 노드를 먼저 우선순위큐에 넣음
while(!pq.empty()) {//우선순위 큐가 빌 때까지 반복
int currentnode = pq.top().first;//우선순위가 제일 높은 노드
int distance = -pq.top().second; //시작노드와의 거리
pq.pop(); //21, 22줄에 다룬 노드를 우선순위 큐에서 제거
if(d[currentnode] < distance) //현 노드의 거리가 전에 저장돼있던 거리보다 멀 때는 다음 루프로 진행
continue;
for(int i=0; i<v[currentnode].size(); i++) { //인접 노드 탐색
int next = v[currentnode][i].first; //인접노드의 정보
int nextdistance = distance + v[currentnode][i].second; //원래 저장돼있던 값에 인접 노드의 거리를 더함
if(nextdistance < d[next]) { //다음 탐색할 노드의 거리가 저장돼있던 거리값보다 작을 때
d[next] = nextdistance; //거리를 새로 갱신
pq.push(make_pair(next, -nextdistance)); //우선순위 큐에 넣어 해당 과정을 반복
}
}
}
}
int main() {
for(int i=1; i<7; i++) { //거리를 무한으로 초기화
d[i]=INF;
}
v[1].push_back(make_pair(2,1));
v[1].push_back(make_pair(4,1));
v[2].push_back(make_pair(3,1));
v[2].push_back(make_pair(5,3));
v[3].push_back(make_pair(2,1));
v[3].push_back(make_pair(6,4));
v[4].push_back(make_pair(1,1));
v[4].push_back(make_pair(5,1));
v[5].push_back(make_pair(2,3));
v[5].push_back(make_pair(6,1));
v[6].push_back(make_pair(3,4));
v[6].push_back(make_pair(6,1));
dijkstra(1);//1노드를 시작 노드로 지정
//1노드와의 거리
for(int i=1; i<7; i++) {
cout << d[i] << ' ';
}
}
'Algorithm' 카테고리의 다른 글
| 동적 계획법, DP(Dynamic Programming) c++ (0) | 2023.04.14 |
|---|---|
| hash map - C++ STL (0) | 2023.03.28 |
| BFS(너비 우선 탐색) 알고리즘 (0) | 2022.07.06 |
| DFS(깊이 우선 탐색) 알고리즘 (0) | 2022.07.04 |
| 투포인터 알고리즘(Two Pointers Algorithm) - c++ (0) | 2022.07.01 |
 >
>
