
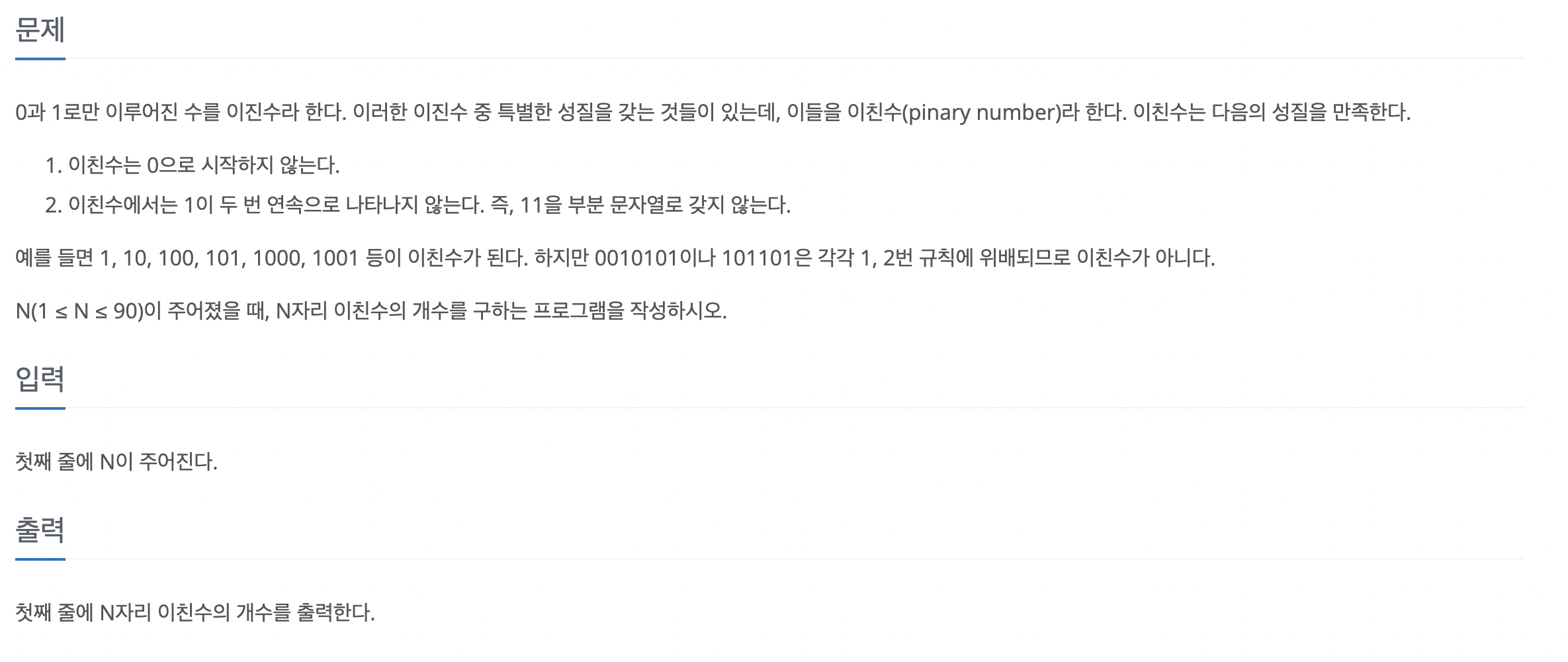
https://www.acmicpc.net/problem/2193
DP알고리즘 문제 같은 경우,
어떤 규칙이 반복되는지만 파악한다면 어렵지않게 문제를 해결해나갈 수 있다.
쓴이는 테스트케이스 1부터 어떤 경우가 나오는지 써가며 푸는 편이다.
N=1 -> 이친수: {1}
N=2 -> 이친수: {10}
N=3 -> 이친수: {100}, {101}
N=4 -> 이친수: {1000}, {1001}, {1010}
N=5 -> 이친수: {10000}, {10001}, {10010}, {10100}, {10101}
N=6 -> 이친수: {100000}, {100001}, {100010}, {100100}, {100101}, {101000}, {101001}, {101010}
.
.
.
테스트 케이스를 살펴보면,
이전 이친수의 끝자리가 0이면 0과 1이 올 수 있고
끝자리가 1이라면 0 하나 밖에 오지 못하는 규칙을 알 수 있다. (1이 중복되면 안되므로)
ex) {10} -> {101}, {100}
{101} -> {1010}
이 규칙을 이용하여
이전 이친수의 끝자리 수 0과 1 각각의 개수를 안다면 그 다음 케이스의 개수도 알 수 있다.
끝자리가 0과 1인 이친수 개수 변수를 각각 first, second라고 가정을 해보자.
| first = 끝자리가 0인 이친수 개수 | second = 끝자리가 1인 이친수 개수 | |
| N=1 | 0 | 1 |
| N=2 | 1 | 0 |
| N=3 | 1 | 1 |
| N=4 | 2 | 1 |
| N=5 | 3 | 2 |
| N=6 | 5 | 3 |
(N>1)일 때
N의 first 값은 (N-1의 first값) + (N-1의 second값)
N의 second 값은 (N-1의 first값)
인 것을 알 수 있다.
#include<iostream>
#include<vector>
#define max 91
using namespace std;
pair <long long, long long> pn[max];
//N이 커질수록 first, second 값이 매우 커지기 때문에 long long 변수로 설정
void pinaryN(int a) {
for(int i=3; i<=a; i++) {
pn[i].first = pn[i-1].first + pn[i-1].second;
pn[i].second = pn[i-1].first;
}
}
int main() {
int N;
///초깃값 설정///
pn[1].first=0; //first는 끝자리가 0인 수
pn[1].second=1; //second는 끝자리가 1인 수
pn[2].first=1;
pn[2].second=0;
///////////////
cin >> N;
pinaryN(N);
cout << pn[N].first + pn[N].second;
}
반응형
'Baekjoon > cpp' 카테고리의 다른 글
| 1697번 - 숨바꼭질 C++ (0) | 2023.07.09 |
|---|---|
| 2178번 - 미로 탐색 C++ (0) | 2023.07.07 |
| 19532번 - 수학은 비대면강의입니다 C++ (0) | 2023.07.03 |
| 2003번 - 수들의 합 2 (0) | 2022.07.04 |
| 1504번 - 특정한 최단 경로 (0) | 2022.06.29 |
 >
>
