
강의 목차
- 심층신경망
- 심층 L 레이어 신경망
- 심층 네트우크에서의 순방향 전파
- 행렬 차원 계산 방법
- 왜 심층 표현인가?
- 심층 신경망의 빌딩 블록
- 순방향 및 역방향 전파
- 파라미터 vs 하이퍼파라미터
- 뇌와 어떤 관련이 있을까?
심층 L 레이어 신경망
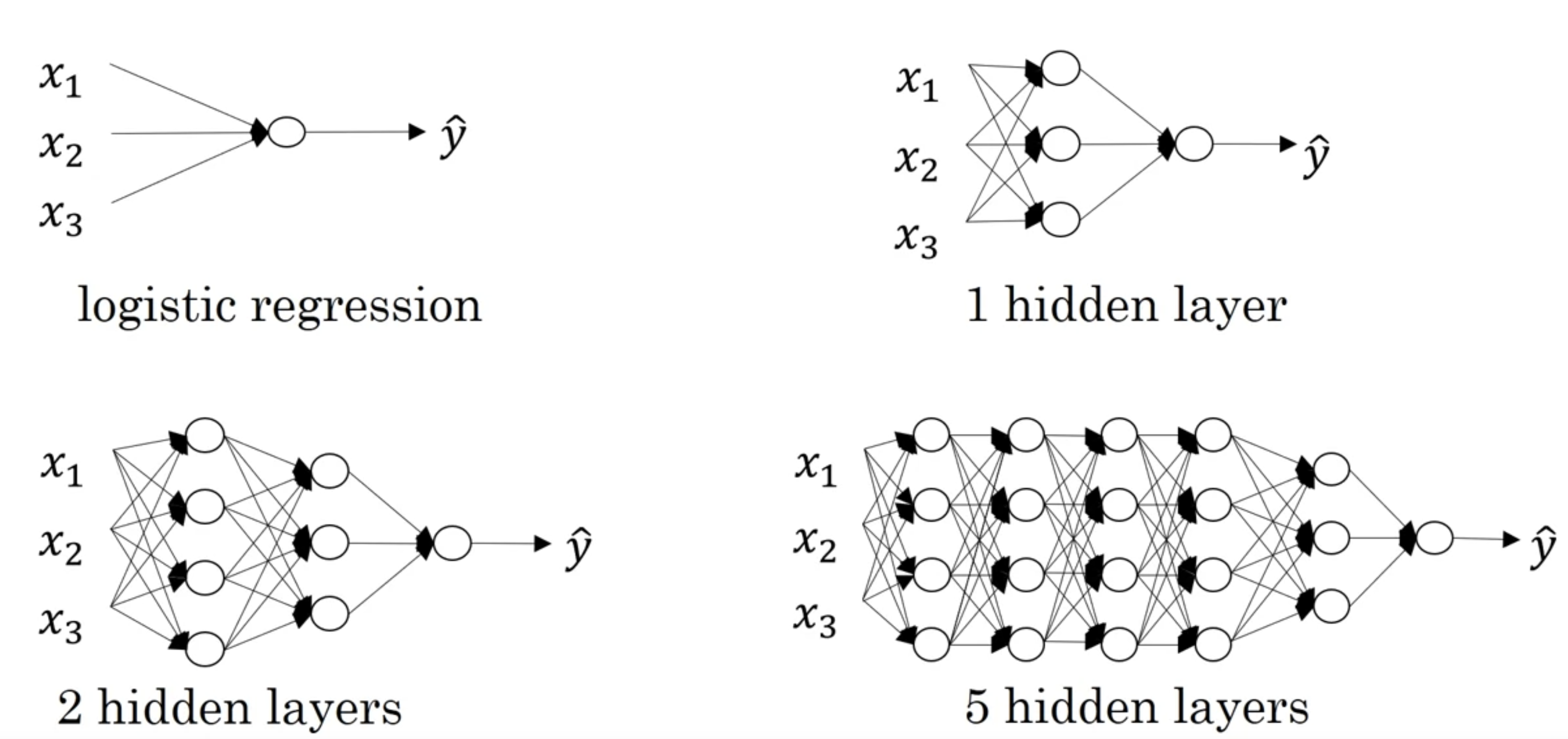
로지스틱 회귀는 얕은 모델
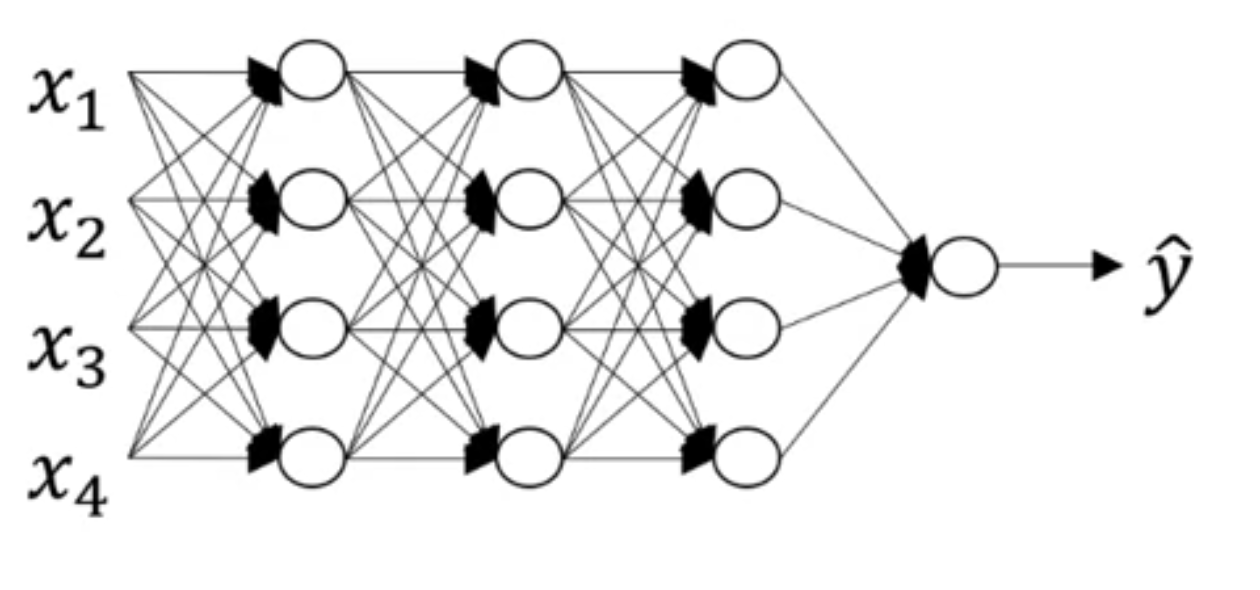
뒤로 갈수록 5 hidden layers는 깊은 모델이라고 할 수 있습니다.
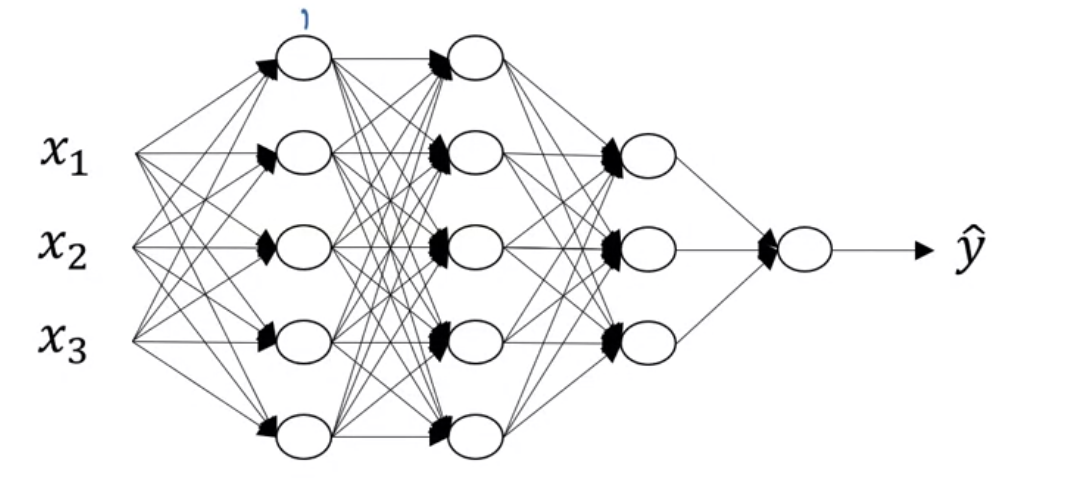
L = 4 (L: 레이어 수, 레이어 수는 입력층을 제외한 나머지 은닉층 + 출력층)
$n^{[l]}$은 layer $l$ 유닛 ex) $n^{[1]}$ = 5
$a^{[l]} = g^{[l]}(z^{[l]})$
$w^{[l]} = z^{[l]}$을 계산하기 위한 가중치
심층 네트워크에서의 순방향 전파
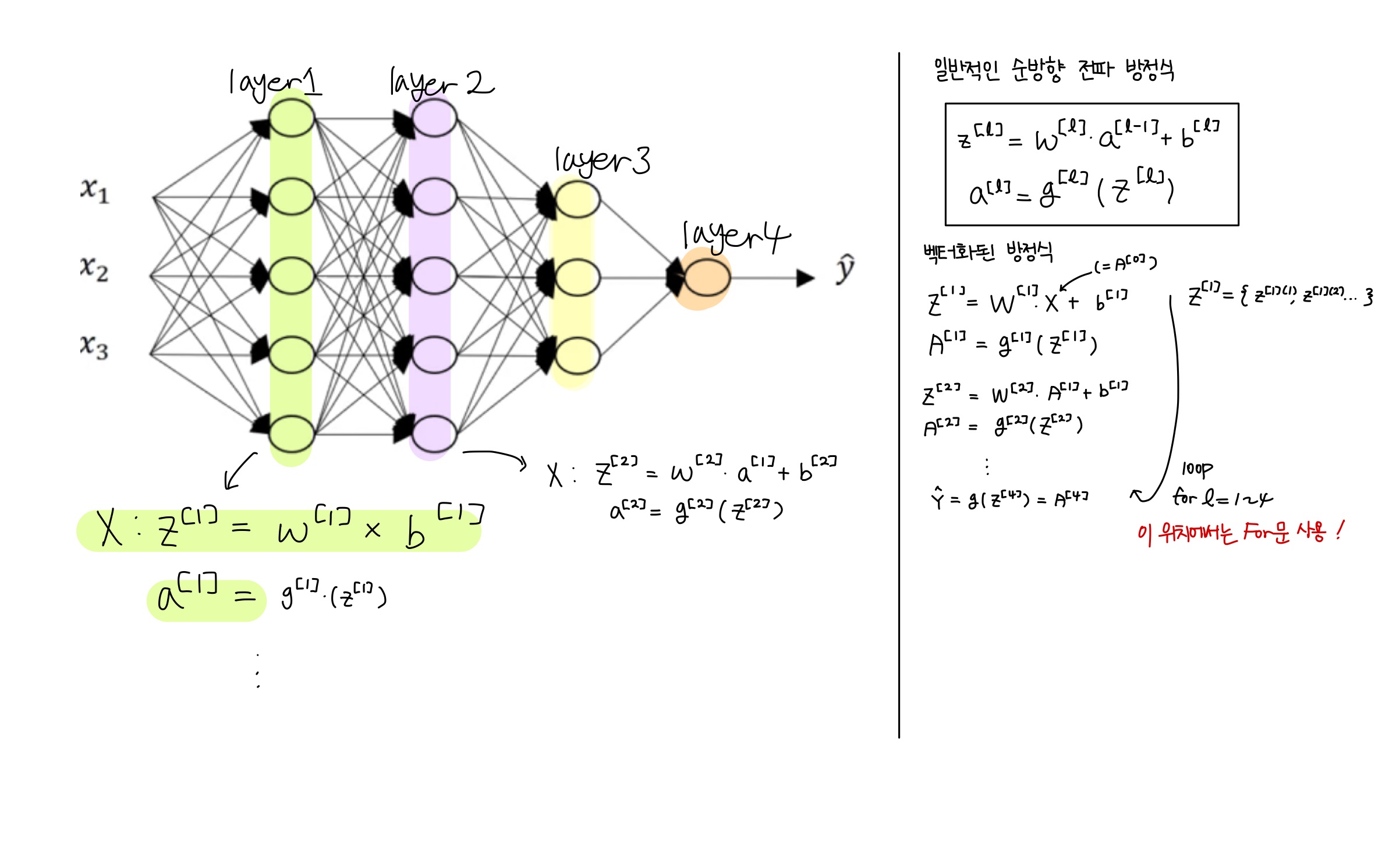
행렬 차원 계산 방법
$z^{[1]} = w^{[1]}*x + b^{[1]}$
$z^{[1]} : (n^{[1]}, 1)$ ----> (3, 1)
$w^{[1]} : (n^{[1]}, n^{[0]})$ ----> (3, 2)
$ x^{[1]} : (n^{[0]}, 1) $ ----> (2, 1)
$ b^{[1]} : (n^{[1]}, 1) $ ----> (3, 1)
$z^{[2]} = w^{[2]}*a^{[1]} + b^{[2]}$
$z^{[2]} : (n^{[2]}, 1)$ ----> (5, 1)
$ w^{[2]} : (n^{[2]}, n^{[1]}) $ ----> (5, 3)
$ b^{[2]} : (n^{[1]}, 1) $ ----> (3, 1)
즉 w와 b는 다음과 같이 정리될 수 있습니다.
$w^{[l]} : (n^{[l]}, n^{[l - 1]})$
$ b^{[l]} : (n^{[l]}, 1)$
역전파 경우에도 차원은 같습니다.
$dw^{[l]} : (n^{[l]}, n^{[l - 1]})$
$db^{[l]} : (n^{[l]}, 1)$
----------------------------------------------------------------------------------------
벡터화 경우는 모두 동일하지만 training set 수 m에 따라 약간 달라집니다.
$z^{[1]} 는 (n^{[1]}, m)$이 됩니다.
$w^{[1]} : (n^{[1]}, n^{[0]})$ ----> (3, 2)
$x^{[1]} : (n^{[0]}, m)$ ----> (2, m)
$b^{[1]} : (n^{[1]}, m)$ ----> (3, m)
$z^{[l], a^{[l]} : (n^{[l]}, 1)$
$Z^{[l]}, A^{[l]} : (n^{[l]}, m)$
dZ와 dA는 Z, A 차원과 동일합니다.
왜 심층표현일까?
심층 신경망의 크기가 크다고 무조건 좋다할 순 없습니다.
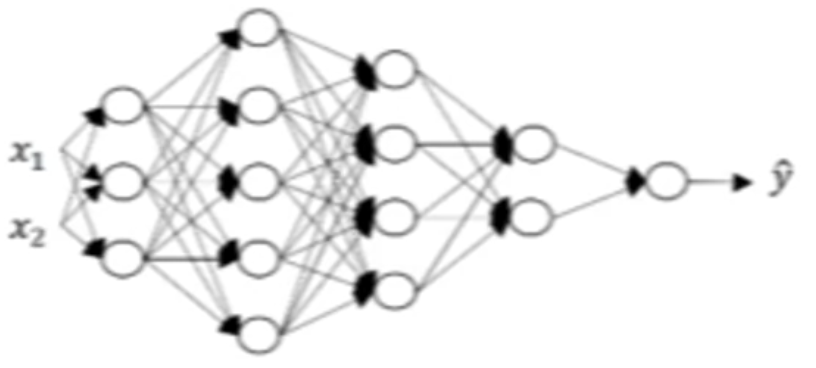
신경망의 네트워크는 깊고 숨겨진 레이어가 많아야 합니다. 그 이유는 다음 그림으로 설명할 수 있습니다.
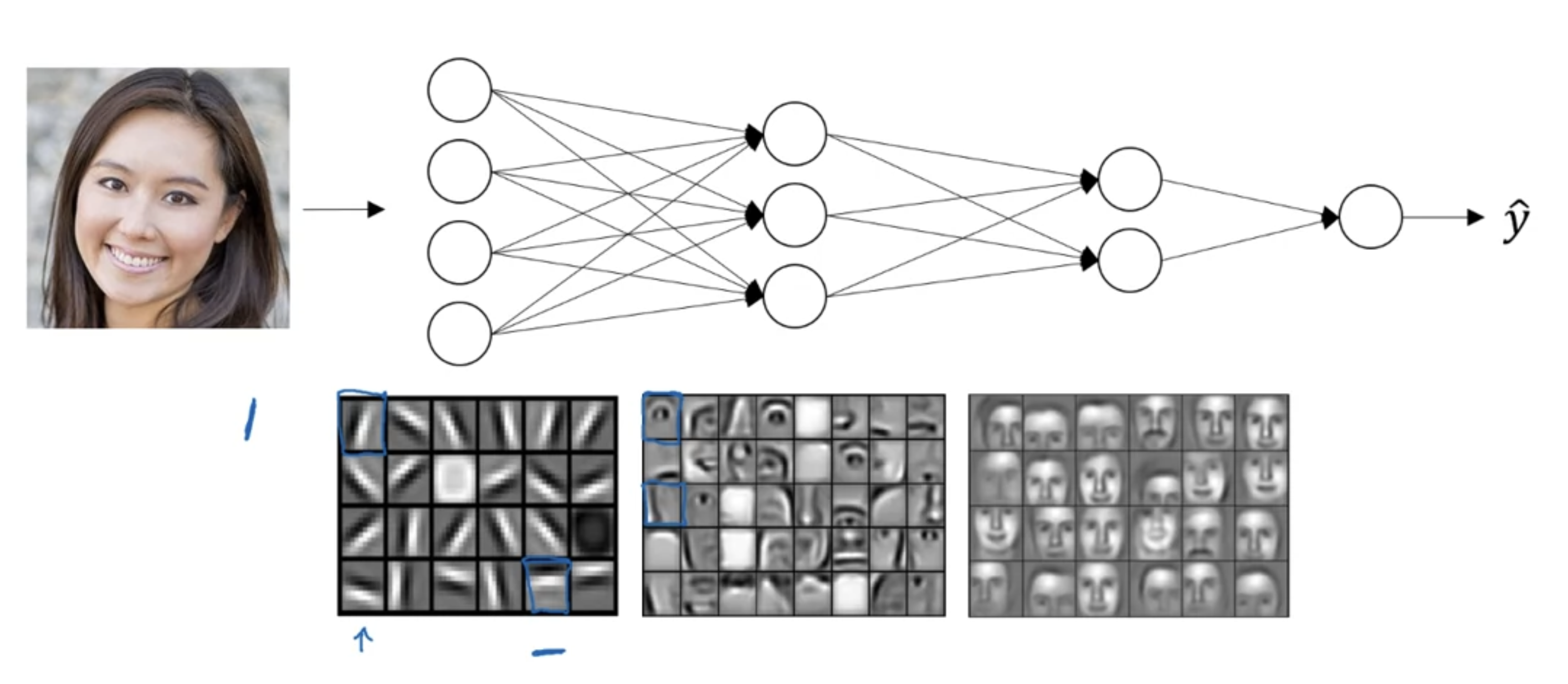
이 예제에서는 24개의 히든 유닛을 가진 신경망이 여자 사진에서 무엇을 계산하려고 하는지를 나타냅니다.
첫 번째 은닉층에서는 아주 작은 단위로 세로 엣지나 가로 엣지의 특성을 파악하고 그 다음 레이어에서는 얼굴 구성 부위 감지, 마지막 레이어에서는 이 전에 파악했던 특성들을 조합한 얼굴 전체 감지 입니다.
중요한 점은 아주 작고 단순한 부분부터 복잡한 부분까지 탐지하기 위해 그것들을 함께 구성하는 것입니다.
Building blocks of deep neural networks
특정 은닉층 하나에 대한 입출력 결과는 이렇습니다.

다음은 전체적인 흐름도 입니다.

맨오른쪽 $da^{[1]}$ 값
$da^{[1]} = \frac{-y}{a} + \frac{(1 - y)}{(1 - a)} $
$dA^{[l]} = (-\frac{y^{(1)}}{a^{(1)}} + \frac{(1 - y^{(1)}}{(1 - a^{(1)})} + \cdots - \frac{-y^{(m)}}{a^{(m)}} + \frac{(1 - y^{(m)}}{(1 - a^{(m)})}) $
순방향 및 역방향 전파



파라미터 vs 하이퍼 파라미터
하이퍼파라미터
- learning rate a
- #terations
- #hidden layers L
- hidden units $n^{[1]}, n^{[2]}, \cdots$
- choice of activation function
데이터
- momentum
- mini-batch
- size
- regulizations, $\cdots$
'Coursera > Neural Networks & Deep Learning' 카테고리의 다른 글
| Neural Networks and Deep Learning [3주차] (1) | 2024.01.11 |
|---|---|
| Neural Networks and Deep Learning [2주차] (2) | 2024.01.04 |
| Neural Networks and Deep Learning [1주차] (0) | 2023.12.30 |
 >
>
![Neural Networks and Deep Learning [4주차]](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fd9oIsQ%2FbtsDp77mqOt%2F38bbeJ9V9OzK82qKkcsezK%2Fimg.png)